Multiplier Block Generator

Explanation

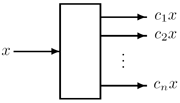
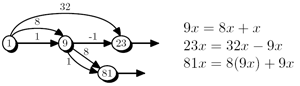
A multiplier block implements a parallel multiplication of a variable with a fixed set of constants. Such multiplier blocks are relevant, for example, for FIR filters. Below we show a general multiplier block and a very simple example - a multiplier block for the parallel multiplication with the constants 23 and 81, generated by our tool [1].

Parallel multiple constant multiplication (MCM)	An example multiplier block, implementing multiplication by 23 and 81

Generation of the minimal cost multiplier block is an NP-complete problem. The currently best heuristic method is provided by our recent paper [1], which also serves as an overview on the best existing methods. Below we provide an online interface to our algorithm (called Hcub) and two competing methods.

Other multiplierless problems

Generator

Input: A list of integer or fixed-point constants c_1, ..., c_n.

Output: Pseudo code and the corresponding directed acyclic graph (DAG) for the multiplier block implementing the parallel multiplications c_1*x, ..., c_n*x. The only operations used in the generated DAG and code are additions, subtractions, shifts and negations (if there are negative constants).

Parameter	Value	Explanation
Constants	0.2303778133088 0.7148465705529 0.6308807679298 0.0279837694168 -0.1870348117190 0.0308413818355 0.0328830116668 -0.0105974017850	Integer or floating point constants. Maximum 20 constants. Floating point constants will be converted into integers using the number of fractional bits given below. Maximum 25 bits after conversion.
Fractional bits	0 (integer constants)    123 456 78 91011 121314 151617 181920 212223 2425	Constants will be scaled by 2^f, where f is the value given here. Use 0 for integer constants.
Algorithm	Hcub (our algorithm)    BHM RAG-n (19 bits max)	MCM algorithm to use. Hcub is our algorithm [1], BHM [3], and RAG-n [3] (limited to 19 bit constants).
Depth limit	Unlimited Minimum possible        1 2 3 4 5 6 7 8 9 10	Maximum allowed adder tree depth. Reducing the depth increases the adder cost. Small depth results in lower latency in hardware.
Secondary optimization	Randomize Reduce adder size (NOFS)	'Randomize' will lead to somewhat different results on every run. 'Reduce adder size' is deterministic and minimizes non-output fundamental sum (NOFS) which is the sum of intermediate constants. This leads to smaller adders in hardware.

Benchmark

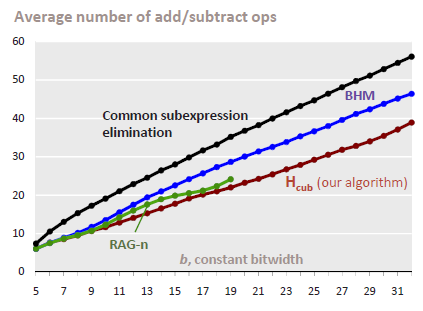
Two example benchmarks from [1]. The plots compare the number of constants (n) and constant bitwidth (b) versus the average number of add/subtract operations in the generated multiplier block for b=19 and n=10, respectively. Note, that we do not count shifts. We compare our new algorithm Hcub [1] to the other algorithms described below.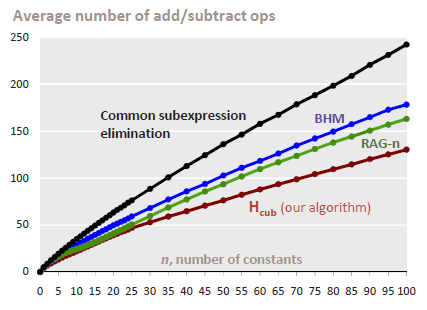

Number of constants vs. op-count for b=19 bits	Constant bitwidth vs. op-count for n=10 constants

• Hcub. New MCM algorithm from our recently accepted paper [1].
• RAG-n. Previously the best published MCM algorithm that we are aware of. We have reimplemented the algorithm, and generated the required lookup table up to 19 bits. Further, we improved the algorithms by inserting our complete A-distance test for distance 2, in which case the original implementation used a heuristic only. RAG-n relies on the availability of optimal single constant decomposition table [4]. RAG-n is described in [3].
• BHM. This is an improved version of the BHA (i.e., the ``add/subtract/shift'' algorithm from [2]. We have implemented this algorithm in C++ using the BHA pseudo-code given in [2] and the BHM improvements from [3].
• Common subexpression elimination. This is one of the newer common subexpression elimination based MCM algorithms by V. Lefèvre [5]. The algorithm uses more sophisticated methods for identifying common subexpressions than those used in previous works. The author has kindly provided us with his implementation.

Software Download

Our software is available under GNU GPL license. Commercial license can be obtained on request.

synth-jan-14-2009.tar.gz (new: depth limits, randomization, NOFS reduction)

synth-feb-20-2006.tar.gz

To use RAG-n download and unzip the file below. Pass the file as an argument to -ac1 option

20min.chains.gz

References

1. Yevgen Voronenko and Markus Püschel 
   Multiplierless Multiple Constant Multiplication 
   ACM Transactions on Algorithms, Vol. 3, No. 2, 2007
   [ Figures (PNG) ]
2. D. R. Bull and D. H. Horrocks
   Primitive operator digital filters
   IEE Proceedings G, 138(3):401-412, 1991
   [ BIB ]
3. A. G. Dempster and M. D. Macleod
   Use of minimum-adder multiplier blocks in FIR digital filters
   IEEE Transactions in Circuits and Systems-II: Analog and Digital Signal Processing, 42(9):569-577, 1995
   [ BIB ]
4. A. G. Dempster and M. D. Macleod.
   Constant integer multiplication using minimum adders
   IEE Proceedings - Circuits, Devices and Systems, 141(5):407-413, 1994
   [ BIB ]
5. V. Lefèvre.
   Multiplication by an integer constant
   Technical report, INRIA, 2001. [ BIB | HTML ]

More information

See also the Spiral Multiplierless Constant Multiplication website.

Copyright (c) 2006-2009 by Yevgen Voronenko for the Spiral project, Carnegie Mellon University

Contact: help at spiral dot net