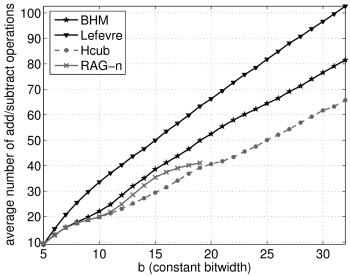
Constant Bitwidth Versus Average Op-count
Plots below compare the constant bitwidth (b) versus the average number of additions (and subtractions) in the generated multiplier block for several choices of constant set sizes (n). Note, that we do not count shifts. We compare our new algorithm (Hcub) desribed here and the algorithms listed below:- RAG-n. Currently the best published MCM algorithm that we are aware of. We have reimplemented the algorithm, and generated the required lookup table up to 19 bits. Further, we improved the algorithms by inserting our complete A-distance test for distance 2, in which case the original implementation used a heuristic only.
- BHM. This is an improved version of the BHA (i.e., the ``add/subtract/shift'' algorithm from \cite{bull91}. We have implemented this algorithm in C++ using the BHA pseudo-code given in \cite{bull91} and the BHM improvements from \cite{dempster95fir}.
- Lefèvre. Described in \cite{lefevre01}, this is one of the newer common subexpression elimination based MCM algorithms. The algorithm uses more sophisticated methods for identifying common subexpressions, but otherwise is similar to \cite{pasko99cse}. The author has kindly provided us with his implementation.
n=1
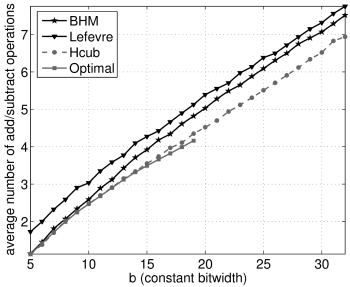
n=2
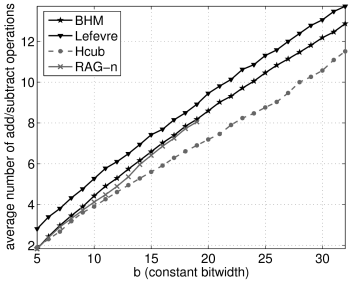
n=10

n=20